Hello Texture#

Introduction#
Up to this point, we have used per-vertex attributes to provide color information for our triangles rendered on the screen. This approach involves associating a color with each vertex of the triangle, allowing the rasterizer to interpolate colors for internal fragments. While this method offers a straightforward way to fill 3D primitives with colors, the visual effect may lack realism.
The goal of this tutorial is to learn how to enhance the level of detail and realism in our meshes by mapping 2D textures onto 3D geometries. To achieve this, we need to switch from setting colors per-vertex to setting colors per-fragment. The upcoming sections will guide you through the necessary steps to make this transition.
Note
Typically, textures are created by graphic artists and provided as assets for use in our graphics applications. However, for the sake of simplicity, in this tutorial we will manually create (i.e., programmatically generated in the source code) a basic texture that exhibits a checkerboard pattern.
Before delving into the code of the sample, it’s crucial to grasp some fundamental theory behind texture mapping. Texture mapping is a technique that allows us to apply an image or pattern onto a 3D mesh, enhancing its visual appearance and adding fine-grained details. With texture mapping, we can achieve more realistic and visually appealing renderings.
See also
Part of the theory illustrated in the following sections draws from the official Microsoft documentation. In particular, [Mica] and [Micb] are used as references.
Textures#
A texture is a resource that can be thought of as an array of contiguous texels (texture elements) stored in memory. Texels are the smallest units of a texture that can be read or written to. When a shader reads a texture, samplers can be used to filter accesses to the texels of the texture. Each texel contains 1 to 4 components (also called channels), arranged in one of the DXGI formats defined by the DXGI_FORMAT enumeration. For example, DXGI_FORMAT_R8G8B8A8_UNORM specifies that every texel is a 32-bit value composed of four 8-bit unsigned-normalized-integer channels. This means that the value of each channel is in the range \([0/255, 255/255]=[0, 1]\); that is, each channel can represent 256 different values (that’s the actual meaning of unsigned-normalized-integer).
Note
Textures are commonly created by graphic artists and supplied in JPEG or PNG format, which are two of the most widely used image file formats. However, to employ these files in DirectX applications, we need additional code or an external library (such as DirectXTK12) to transform the image data into a supported DXGI format before creating the actual texture resource.
As an alternative, graphic artists or programmers can convert the image data into a supported DXGI format and store the (compressed or uncrompressed) result in a specialized container file. These container files, such as DDS (DirectDraw Surface), encapsulate the texture type and data, along with additional information like format, dimensions, and mipmap levels. This approach ensures optimal performance for runtime usage and supports a variety of texture resource types and formats (1D, 2D, volume maps, cubemaps, mipmap levels, texture arrays, cubemap arrays, block compressed formats, etc.). More details on texture containers will be provided in a later tutorial.
1D Textures#
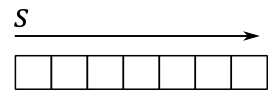
A 1D texture, in its simplest form, can be visualized as an array of contiguous texels in memory. In this case, the texture data can be addressed with a single coordinate (s in the image below).
Adding more complexity, we can also create a 1D texture with mipmap levels, as shown in the following image.
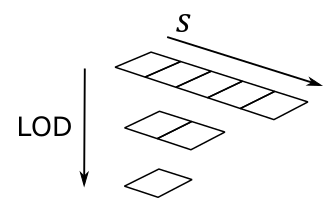
Just think of it as a single resource that is made up of three subresources. Mipmaps play a crucial role in texture sampling and filtering by providing smaller versions of the original image. The highest level, known as level 0, include the original image and holds the finest level of detail. As we move down the hierarchy, each subsequent level contains a progressively smaller mipmap with reduced details.
For a 1D texture with mipmaps, the smallest level contains a mipmap composed of one texel. Mipmaps are generated by halving the size of the previous level, rounding up to the nearest even integer, until we get a mipmap of a single texel. For example, the illustration above shows a \(5\times 1\) texture whose next lower mipmap is a \(2\times 1\) texture, whose next (and last) mipmap is a \(1\times 1\) sized texture.
To facilitate identification and retrieval of specific subresources during geometry rendering based on camera distance, each level is assigned an index, commonly referred to as LOD (level-of-detail). This LOD index serves as a useful tool for accessing the appropriate mipmap level when required.
1D Texture arrays#
Direct3D also supports arrays of textures. An array of 1D textures looks conceptually like the following illustration.
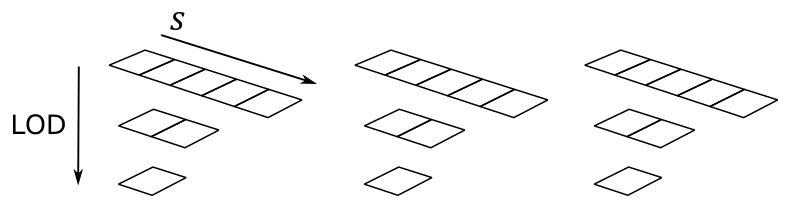
The above texture array contains three textures, each containing three mipmaps. So, you can also consider it as a single resource that is made up of nine subresources.
Typically, texture array include homogeneous elements. This means that all textures in the array must have the same format, size, and number of mipmap levels. The size of a texture array is set to the dimension of the topmost mipmap level. For example, the size of the texture array illustrated above is 5 because the topmost mipmap of each texture includes five texels.
2D Textures and 2D Texture arrays#
A 2D Texture can be conceptually visualized as a 2D grid of texels — although it is physically stored as an array of contiguous texels, just like 1D textures. This grid-like (logical) arrangement facilitates addressing individual texels using two coordinates (s and t in the image below), enabling efficient access and manipulation of texels within the texture. Similar to 1D textures, 2D textures may contain mipmap levels. An example of 2D texture resource (with mipmaps) is illustrated in the following image.
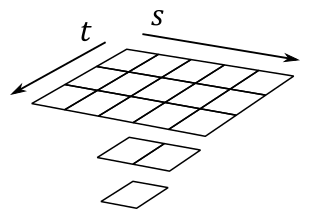
The texture above has a \(3\times 5\) mipmap at the topmost level, along with two other smaller mipmaps at lower levels.
A 2D texture array resource is a homogeneous array of 2D textures; that is, each texture has the same data format and dimensions (including mipmap levels). It has a similar layout as the 1D texture array, except that the textures now contain 2D data, as shown in the following illustration.
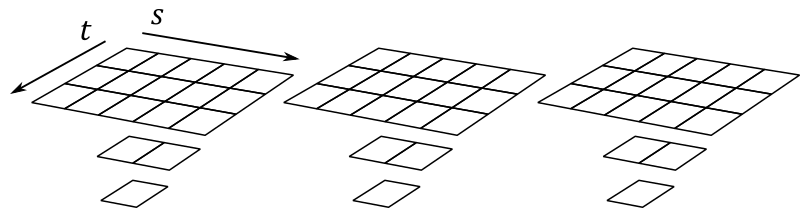
The array texture illustrated above contains three textures, each with a \(3\times 5\) mipmap at the topmost level, and with two additional smaller mipmaps at lower levels. So, you can also consider it as a single resource made up of nine subresources.
Note
3D textures exist as well, but we’ll leave the discussion of 3D textures for a subsequent tutorial.
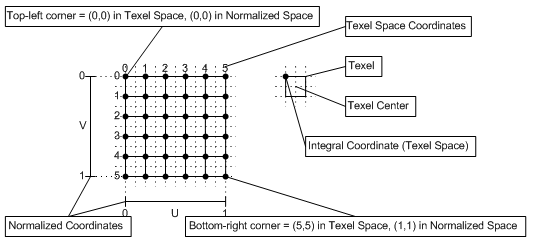
Texel Coordinate System#
The texel coordinate system has its origin at the top-left corner of the texture, as shown in the following diagram. Texel coordinates \((s,t)\) are typically continuous, but texels are usually located at integer locations (discrete coordinates). In this space, texel centers are offset by \((0.5, 0.5)\) (half-integer locations). Normalized coordinates in the following illustration below contribute to a better understanding of the relationship between the texel and texture coordinate systems (explained in more detail in the subsequent sections).
Texture Coordinate System#
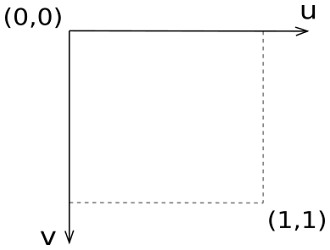
As stated in the previous section, each texel in a texture can be specified by its integer texel coordinates. However, in order to map texels onto primitives, Direct3D requires a uniform address range. That is, it uses a generic addressing scheme in which each component of all texel addresses \((s,t)\) is normalized to be within the range \([0.0,\ 1.0]\).
Note
Technically, Direct3D can actually process texture coordinates outside the range \([0, 1]\). The way it handles these coordinates depends on the parameters you set for texture addressing (more on this shortly).
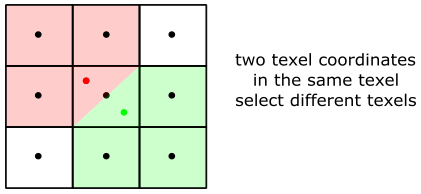
With texture coordinates, we can address texels without knowing the size of a texture. For example, in the following illustration, we can select the central texel in the last row for two different textures by using the texture coordinates \((0.5, 1.0)\).
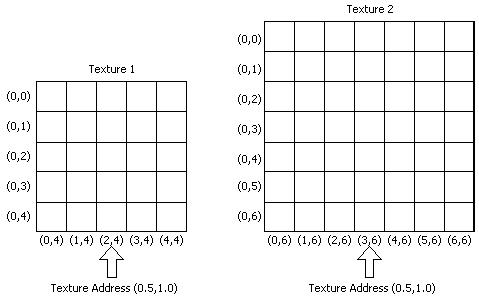
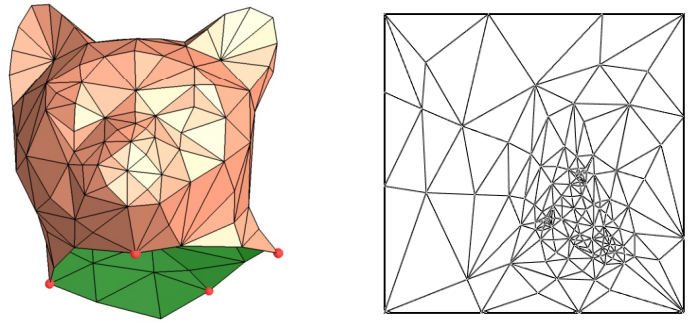
Applying a texture to a 3D primitive involves mapping texel coordinates to the vertices of the primitive. However, how can we map 2D texel coordinates to 3D positions? One way to do that is through a technique called UV mapping, which conceptually involves unwrapping the 3D mesh onto the unit square \([0,1]\times [0,1]\) that defines the texture coordinate system. This process is similar to unwrapping a Christmas chocolate on a table, as illustrated below.

UV mapping allows vertex positions to be associated with texture coordinates within the unit square defined above. This ends up allowing us to determine which texel from the texture will be mapped to a specific vertex position. We’ll demonstrate this soon with a straightforward example.
Here, for the sake of semplicity, we will consider a single triangle that is mapped to take the whole unit square of texture coordinate system.
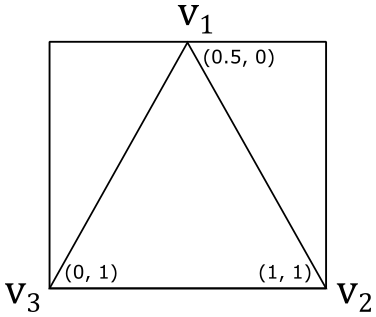
By associating (using vertex attributes in the definition of the corresponding vertex buffer) the texture coordinates \((0.5, 0)\), \((1, 1)\) and \((0, 1)\) respectively with the vertices \(\mathbf{v}_1\), \(\mathbf{v}_2\) and \(\mathbf{v}_3\) of a triangle in 3D space, we establish a connection between vertex positions and texture coordinates. To obtain the integer texel coordinates that allow us to select a texel from the texture, we can multiply each component of the texture coordinates by the corresponding dimension of the texture, minus 1, and round the result by simply truncating the fractional part.
For example, if we have an \(8\times 4\) texture, the vertex \(\mathbf{v}_1\) in the figure above would be paired with the integer texel coordinates \(\big(⌊(0.5∗(8-1))⌋,\ ⌊(0.0∗(4-1))⌋\big)=(3,0)\). This way, we associated the vertex position \(\mathbf{v}_1\) with the fourth texel of the first row of the texture. The same goes for the vertices \(\mathbf{v}_2\) and \(\mathbf{v}_3\), which would be associated respectively with the last and first texels of the last row. Eventually, we established a connection between vertices and texels.
This association between vertices and texels allows us to enhance the level of detail and realism in our rendering. How? Well, first of all, it should be noted that associating vertices with texels practically means that we must declare the texture coordinates as a vertex attribute to associate them with vertex positions in 3D space. When the rasterizer interpolates the texture coordinates of a pixel, we can use the result in the shader code to select a texel from a texture as the per-pixel color (more on this shortly). This means that instead of having an interpolated color for each pixel within a primitive, we now have a color selected from a texture that represents a real material. This allows us to select a color per-pixel rather than per-vertex, leading to an higher level of detail and realism.
Sampling#
In the context of texture mapping, sampling refers to the process of retrieving data from a texture using a sampler, which allows to look up texel values from their texture coordinates.
In theory, it would be possible to associate vertex positions in the vertex buffer with texture coordinates that always translate to integer texel coordinates. However, even in that case, the rasterizer will likely emit pixels with interpolated texture coordinates that do not translate to integer texel coordinates.
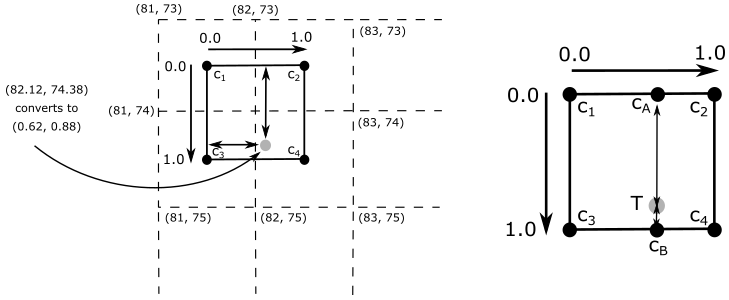
For example, consider the generic interpolated texture coordinates \((u, v)\) which translate to the texel coordinates \((s, t) = (82.12, 74.38)\) as shown in the illustration above. Now, a question arises: which texel should be selected in this case? To address this issue, we require a sampler that, among its various properties, specifies a filter for texel selection.
There are three filters available for texel selection: point, linear and anisotropic (we will cover the anisotropic filter in a later tutorial).
Point filtering means that the selected texel is the nearest one, computed by simply truncating the fractional part from texel coordinates. So, in the case illustrated above, the selected texel will be the one with texel coordinates \((82,74)\). That is, the one with center in \(\mathbf{c}_4\).
Linear filtering means that we select the four nearest texels to interpolate their values. In this case, it is preferable to consider the centers of the texels for the texel selection. The reason for this is that the calculation of the four texels is computed by simply dropping the fractional part and increasing the components of the texel coordinates, that is: \((⌊x⌋,\ ⌊y⌋)\), \((⌊x⌋+1,\ ⌊y⌋)\), \((⌊x⌋,\ ⌊y⌋+1)\) and \((⌊x⌋+1,\ ⌊y⌋+1)\). That way, if we were to use the texel coordinates in this calculation, we might not select the nearest texels. For example, in the case illustrated above, the four selected texels would range from \((82, 74)\) to \((83, 75)\), which are not the nearest ones. The nearest texels actually range from \((81, 73)\) to \((82, 74)\). So how can we select them? We need to convert the texel coordinates to consider their location relative to the coordinate system formed by the four nearest texel centers. This can be done by subtracting \(0.5\) from both components of the texel coordinates. For example, \((82.12, 74.38)–(0.5, 0.5)=(81.62, 73.88)\). This way, the nearest texels range exactly from \((81, 73)\) to \((82,74)\). Now, retaining only the fractional parts we have that \((81.62, 73.88)\) converts to \((0.62, 0.88)\). That’s the exact location of texel coordinates \((s, t)\) in the \([0,1]\times [0,1]\) square formed by the four nearest texel centers. Eventually, we can interpolate their values as follows:
\(\mathbf{c}_A=38\\%\) of \(\mathbf{c}_1+62\\%\) of \(\mathbf{c}_2\)
\(\mathbf{c}_B=38\\%\) of \(\mathbf{c}_3+62\\%\) of \(\mathbf{c}_4\)
\(\mathbf{C}=12\\%\) of \(\mathbf{c}_A+78%\) of \(\mathbf{c}_B\)
This way, we obtain a color \(\mathbf{C}\) starting from the interpolated texel coordinates provided by the rasterizer. Observe that we linearly interpolated between the horizontal texels in the \(4\times 4\) block of nearest texels using the fractional part that corresponds to the s-coordinate, and then we linearly interpolated the results (\(\mathbf{c}_A\) and \(\mathbf{c}_B\)) vertically using the fractional part that corresponds to the t-coordinate. In other words, we performed a bilinear interpolation. Additional information on linear and bilinear interpolation will be provided as an appendix in a later tutorial.
Note
The mapping from texture coordinates to the color returned by a texture fetch instruction in a shader program is an operation automatically performed by the GPU and is transparent to the programmer, who only needs to specify a filter in a sampler. However, knowing the low-level details can prove to be beneficial in the future.
Magnification#
Using a point filter can lead to ugly visual effects (artifacts) during magnification.
Imagine zooming in on a 3D textured mesh until it covers an area of \(1024\times 1024\) pixels on your screen. What happens if the texture of this mesh is, for example, \(64\times 64\)? Well, that means that we have approximately \(1024/64=16\) pixels for each texel, as shown in the following illustration.
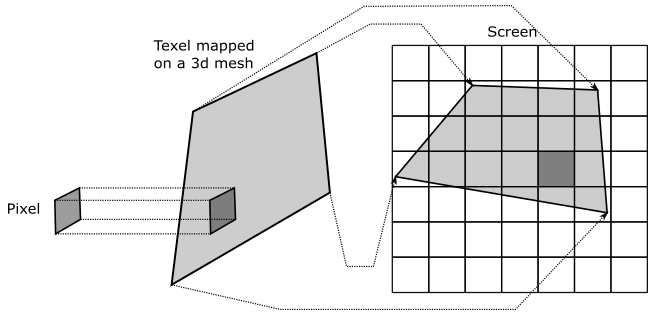
Now, imagine that pixels on your screen were stickers you can shoot straight at the surface of a mesh. This means that, in the case illustrated above, you need to shoot about 16 pixels to cover a single texel. The distortion of the texel may depend on the shape of the mesh and the viewing angle, but we can ignore that for now. What’s important here is that, if we move from a pixel to the next one on the screen, we don’t necessarily move from a texel to another in the texture. That means that the texture coordinates of many pixels will be mapped to the same texel (i.e., to its integer texel coordinates).
Note
Another way to think about it is this: if you zoom in on a 3D textured mesh, then big triangles will likely be projected onto the projection window. Since interpolation is performed by the rasterizer using barycentric coordinates (more on this in a later tutorial), texture coordinates of adjacent fragments won’t change much. Therefore, if the texture is small, many pixels will fall into the same texel area after being converted from texture to texel coordinates.
Visually, this can lead to a blocky effect, as shown in the following illustration (on the left), where many pixels display the same color sampled from the same texel.

You can mitigate this problem by using a linear filter (the result is shown in the image above, on the right). That way, we don’t select the same texel, but rather we interpolate between four texels in the \(3\times 3\) block surrounding it. That is, the interpolated texture coordinates of a pixel translate to texel coordinates within four texel centers that can vary, as shown in the illustration below. This results in a smoother transition between texels and can improve the visual quality of magnified textures.
Minification#
It’s also interesting to consider what happens, using a point filter, during minification, when you zoom out to expand the viewing area. Imagine shooting a pixel straight at a mesh that, this time, is far away from the camera. Now, a single pixel can cover lots of texels.
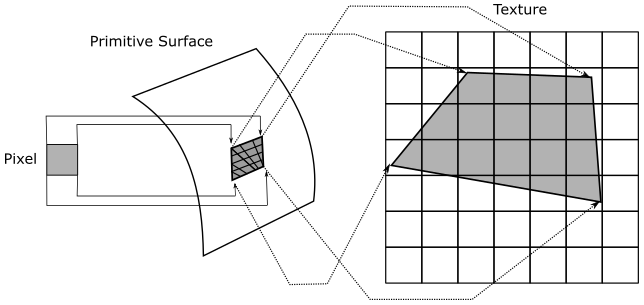
As we know, the color of a pixel depends on the selected texel, calculated from the interpolated texture coordinates associated with the pixel. If we have lots of texels mapped to a single pixel, then the selected texel can randomly vary from a frame to another, even if the mesh moves only slightly (less than a pixel). For example, in the case illustrated above, moving the primitive to the right or left by half a pixel would change approximately half of the texels covered by the pixel. This means that the texture coordinates of the pixel can be mapped to different texels (integer texel coordinates) during this little movement. This can lead to display flickering caused by pixels that rapidly change their color. Using a linear filter can help mitigate this issue, but it doesn’t completely solve it since the four nearest texels can also change rapidly.
Note
Another way to think about it is this: if you zoom out until a textured mesh is far away from the camera, then small triangles will likely be projected onto the projection window. Since interpolation is performed by the rasterizer using barycentric coordinates (more on this in a later tutorial), texture coordinates of adjacent pixels will likely differ significantly from each other. At that point, if the texture is big enough, adjacent pixels can select distant texels in the texture. This means that if a mesh moves slightly (less than a pixel), the interpolated texture coordinates can vary enough to selected different texels for the same pixel on the screen, leading to display flickering.
Fortunately, mipmap levels provide a way to select the texture that best matches the area covered by the mesh on the screen, allowing for a mapping as close to 1:1 as possible between pixels and texels. This can help reduce artifacts caused by minification. For this purpose, in a sampler we can also specify a filter for mipmap selection (in addition to the one for texel selection). A point filter (for mipmap selection) selects the mipmap whose texels are closest in size to screen pixels, while a linear filter selects the two mipmaps that provide the best match. From these two mipmaps, two texels (one from each mipmap) are sampled using the filter for texel selection. These two texels are then interpolated to return the final result (color or other data).
Note
Do you recall our discussion about how blocks of \(2\times 2\) pixels are processed in parallel by the pixel shader? Well, this allows the GPU to calculate the change in interpolated texture coordinates of a pixel relative to its companion pixels in the block. As a result, a LOD index can be computed from this information to select the most appropriate mipmap level. Further details on this topic will be provided in a later tutorial.
Addressing Modes#
Typically, the u and v components of texture coordinates range from \(0.0\) to \(1.0\). However, extending beyond this range can create unique texturing effects. To control how the Direct3D will handle texture coordinates outside of the range, we can set a texture addressing mode for each component. For example, you can set the texture addressing mode so that a texture is tiled across a primitive. For this purpose, Direct3D only need to find a way to map texture coordinates outside the unit square back to \([0.0, 1.0]\). There are various methods to restrict coordinates in a specific range.
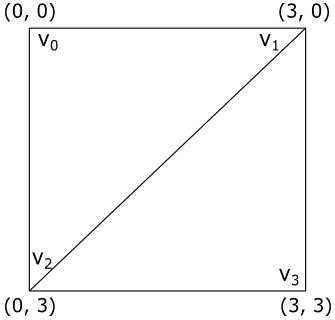
In this section we will only focus on the u-coordinate, but the same applies to the v-coordinate. Additionally, we will assume that we want to draw a quad consisting of two triangles. The vertex positions of the first triangle, \(\triangle_1=(v0, v1, v2)\), are associated with texture coordinates of \((0.0, 0.0)\), \((3.0, 0.0)\) and \((0.0, 3.0)\) respectively, while the positions of the second triangle, \(\triangle_2=(v1, v3, v2)\), are associated with texture coordinates of \((3.0, 0.0)\), \((3.0, 3.0)\) and \((0.0, 3.0)\). The vertices are in clockwise order. The following illustration shows the quad in a \([0,3]\times [0,3]\) square, which extends the \([0,1]\times [0,1]\) square representing the usual texture space.
Wrap#
This addressing mode repeats the texture on every integer junction by using the following function to transform the u-coordinate.
\(\text{wrap}(u) = u – \text{floor}(u)\)
So, in our example, setting the addressing mode to “Wrap” for both the u- and v-coordinates results in the texture being applied three times in both the u and v directions, as shown in the following illustration. The reason is that when, for example, the interpolated texture coordinate u is \(3.0\), \(\text{wrap}(3.0)\) returns \(1.0\). The same happens when u is \(2.0\) and (obviously) \(1.0\).

Mirror#
This addressing mode mirrors and repeats the texture at every integer boundary by using the following function to transform the u-coordinate.
\(\text{mirror}(u)= \begin{cases} u-\text{floor}(u), & \text{floor}(u) \% 2=0 \\ \text{floor}(u+1)-u, & \text{floor}(u) \% 2=1 \end{cases}\)
Setting the texture addressing mode to “Mirror” results in the texture being applied three times in both the u and v directions. Observe that every other row and column that it is applied to is a mirror image of the preceding row or column, as shown in the following illustration. The reason is that when, for example, the interpolated texture coordinate u is \(3.0\), \(\text{mirror}(3.0)\) returns \(1.0\) while when u is \(2.0\) it returns \(0.0\).

Clamp#
This addressing mode clamps the u-component of the texture coordinate to the \([0.0,\ 1.0]\) range by using the following function.
\(\text{clamp}(u) = \text{max}(\text{min}(u, 1), 0)\)
Setting the texture addressing mode to “Clamp” applies the texture once, then smears the color of edge texels. In the following illustration the edges of the texture are delimited with a light grey square.

Border#
Setting the texture addressing mode to “Border” means we want to use an arbitrary color, known as the border color, for any texture coordinates outside the range of \(0.0\) through \(1.0\), inclusive. We can set the border color in the sampler. The following illustration shows a texture (on the left), and its mapping to our quad (on the right) when a red border color is specified in the sampler.

D3D12HelloTextures: code review#
In this section, we will review the code of a sample that draws a textured triangle. The image below shows the texture we will map to this basic mesh. The texture presents a classic checkerboard pattern, alternating between black and white squares. As mentioned earlier in this tutorial, textures are typically created by graphic artists. However, in this case, the pattern of the texture is regular enough to be manually generated.

C++#
As usual, let’s start from the application class.
class D3D12HelloTexture : public DXSample
{
public:
D3D12HelloTexture(UINT width, UINT height, std::wstring name);
virtual void OnInit();
virtual void OnUpdate();
virtual void OnRender();
virtual void OnDestroy();
private:
static const UINT FrameCount = 2;
static const UINT TextureWidth = 256;
static const UINT TextureHeight = 256;
static const UINT TexturePixelSize = 4; // The number of bytes used to represent a pixel\texel in the texture.
struct Vertex
{
XMFLOAT3 position;
XMFLOAT2 uv;
};
// Pipeline objects.
CD3DX12_VIEWPORT m_viewport;
CD3DX12_RECT m_scissorRect;
ComPtr<IDXGISwapChain3> m_swapChain;
ComPtr<ID3D12Device> m_device;
ComPtr<ID3D12Resource> m_renderTargets[FrameCount];
ComPtr<ID3D12CommandAllocator> m_commandAllocator;
ComPtr<ID3D12CommandQueue> m_commandQueue;
ComPtr<ID3D12RootSignature> m_rootSignature;
ComPtr<ID3D12DescriptorHeap> m_rtvHeap;
ComPtr<ID3D12DescriptorHeap> m_srvHeap;
ComPtr<ID3D12PipelineState> m_pipelineState;
ComPtr<ID3D12GraphicsCommandList> m_commandList;
UINT m_rtvDescriptorSize;
// App resources.
ComPtr<ID3D12Resource> m_vertexBuffer;
D3D12_VERTEX_BUFFER_VIEW m_vertexBufferView;
ComPtr<ID3D12Resource> m_texture;
// Synchronization objects.
UINT m_frameIndex;
HANDLE m_fenceEvent;
ComPtr<ID3D12Fence> m_fence;
UINT64 m_fenceValue;
void LoadPipeline();
void LoadAssets();
std::vector<UINT8> GenerateTextureData();
void PopulateCommandList();
void WaitForPreviousFrame();
};
We will use a texture of \(256\times 256\) texels, where the size of each texel is 4 bytes. We will use this information to determine the amount of GPU heap space to allocate for the texture.
The Vertex structure (that describe the elements of the vertex buffer) now uses texture coordinates (rather than a color) as a vertex attribute. That way, we can go from selecting a color per-vertex to selecting a color per-pixel, increasing the level of detail and realism.
We will use the m_texture variable to reference the texture from our C++ application, and m_srvHeap to create a descriptor heap that will hold a view to the texture.
GenerateTextureData is the method that procedurally generates the checkerboard texture data, texel by texel.
// Generate a simple black and white checkerboard texture.
std::vector<UINT8> D3D12HelloTexture::GenerateTextureData()
{
const UINT rowPitch = TextureWidth * TexturePixelSize;
const UINT cellPitch = rowPitch >> 3; // The width of a cell in the checkerboard texture.
const UINT cellHeight = TextureWidth >> 3; // The height of a cell in the checkerboard texture.
const UINT textureSize = rowPitch * TextureHeight;
std::vector<UINT8> data(textureSize);
UINT8* pData = &data[0];
for (UINT n = 0; n < textureSize; n += TexturePixelSize)
{
UINT x = n % rowPitch;
UINT y = n / rowPitch;
UINT i = x / cellPitch;
UINT j = y / cellHeight;
if (i % 2 == j % 2)
{
pData[n] = 0x00; // R
pData[n + 1] = 0x00; // G
pData[n + 2] = 0x00; // B
pData[n + 3] = 0xff; // A
}
else
{
pData[n] = 0xff; // R
pData[n + 1] = 0xff; // G
pData[n + 2] = 0xff; // B
pData[n + 3] = 0xff; // A
}
}
return data;
}
The rowPitch variable represents the byte size of a texture row, calculated as TextureWidth * TexturePixelSize \((256∗4=1024)\). The cellPitch variable represents the width of a checkerboard cell in bytes, calculated as rowPitch >> 3 \((1024/8=128)\). This means that each row has 8 cells, where each cell includes \((128/4)= 32\) texels. The height of each cell is calculated as TextureWidth >> 3 \((256/8=32)\), which means each cell includes 32 texels as well. Observe that the cell height is measured in texels, not bytes like the cell width. This is because we will use the local variable j to count the texels of a cell vertically while the local variable i to count the bytes of a cell horizontally. These two variables, along with the loop counter n, play a crucial role in alternating between black and white cells. In partcular, for each texel, the function sets the RGBA values to either 0x00 or 0xFF depending on whether (i % 2 == j % 2). This creates a checkerboard pattern with black and white cells.
Now, let’s take a look at the LoadPipeline function.
// Load the rendering pipeline dependencies.
void D3D12HelloTexture::LoadPipeline()
{
// ...
// Create descriptor heaps.
{
// Describe and create a render target view (RTV) descriptor heap.
D3D12_DESCRIPTOR_HEAP_DESC rtvHeapDesc = {};
rtvHeapDesc.NumDescriptors = FrameCount;
rtvHeapDesc.Type = D3D12_DESCRIPTOR_HEAP_TYPE_RTV;
rtvHeapDesc.Flags = D3D12_DESCRIPTOR_HEAP_FLAG_NONE;
ThrowIfFailed(m_device->CreateDescriptorHeap(&rtvHeapDesc, IID_PPV_ARGS(&m_rtvHeap)));
// Describe and create a shader resource view (SRV) heap for the texture.
D3D12_DESCRIPTOR_HEAP_DESC srvHeapDesc = {};
srvHeapDesc.NumDescriptors = 1;
srvHeapDesc.Type = D3D12_DESCRIPTOR_HEAP_TYPE_CBV_SRV_UAV;
srvHeapDesc.Flags = D3D12_DESCRIPTOR_HEAP_FLAG_SHADER_VISIBLE;
ThrowIfFailed(m_device->CreateDescriptorHeap(&srvHeapDesc, IID_PPV_ARGS(&m_srvHeap)));
m_rtvDescriptorSize = m_device->GetDescriptorHandleIncrementSize(D3D12_DESCRIPTOR_HEAP_TYPE_RTV);
}
// ...
}
We need a descriptor heap to hold the SRV we are about to create as a view for the texture. This is not much different from what we have seen in Hello Constant Buffers (we simply renamed m_cbvHeap to m_srvHeap). Remember that a descriptor heap of type D3D12_DESCRIPTOR_HEAP_TYPE_CBV_SRV_UAV can hold both CBVs and SRVs.
The LoadAssets function has grown considerably in this sample, but there’s no need to worry. We will carefully review all the code in detail.
// Load the sample assets.
void D3D12HelloTexture::LoadAssets()
{
// Create the root signature.
{
D3D12_FEATURE_DATA_ROOT_SIGNATURE featureData = {};
// This is the highest version the sample supports. If CheckFeatureSupport succeeds, the HighestVersion returned will not be greater than this.
featureData.HighestVersion = D3D_ROOT_SIGNATURE_VERSION_1_1;
if (FAILED(m_device->CheckFeatureSupport(D3D12_FEATURE_ROOT_SIGNATURE, &featureData, sizeof(featureData))))
{
featureData.HighestVersion = D3D_ROOT_SIGNATURE_VERSION_1_0;
}
CD3DX12_DESCRIPTOR_RANGE1 ranges[1];
ranges[0].Init(D3D12_DESCRIPTOR_RANGE_TYPE_SRV, 1, 0, 0, D3D12_DESCRIPTOR_RANGE_FLAG_DATA_STATIC);
CD3DX12_ROOT_PARAMETER1 rootParameters[1];
rootParameters[0].InitAsDescriptorTable(1, &ranges[0], D3D12_SHADER_VISIBILITY_PIXEL);
D3D12_STATIC_SAMPLER_DESC sampler = {};
sampler.Filter = D3D12_FILTER_MIN_MAG_MIP_POINT;
sampler.AddressU = D3D12_TEXTURE_ADDRESS_MODE_BORDER;
sampler.AddressV = D3D12_TEXTURE_ADDRESS_MODE_BORDER;
sampler.AddressW = D3D12_TEXTURE_ADDRESS_MODE_BORDER;
sampler.MipLODBias = 0;
sampler.MaxAnisotropy = 0;
sampler.ComparisonFunc = D3D12_COMPARISON_FUNC_NEVER;
sampler.BorderColor = D3D12_STATIC_BORDER_COLOR_TRANSPARENT_BLACK;
sampler.MinLOD = 0.0f;
sampler.MaxLOD = D3D12_FLOAT32_MAX;
sampler.ShaderRegister = 0;
sampler.RegisterSpace = 0;
sampler.ShaderVisibility = D3D12_SHADER_VISIBILITY_PIXEL;
CD3DX12_VERSIONED_ROOT_SIGNATURE_DESC rootSignatureDesc;
rootSignatureDesc.Init_1_1(_countof(rootParameters), rootParameters, 1, &sampler, D3D12_ROOT_SIGNATURE_FLAG_ALLOW_INPUT_ASSEMBLER_INPUT_LAYOUT);
ComPtr<ID3DBlob> signature;
ComPtr<ID3DBlob> error;
ThrowIfFailed(D3DX12SerializeVersionedRootSignature(&rootSignatureDesc, featureData.HighestVersion, &signature, &error));
ThrowIfFailed(m_device->CreateRootSignature(0, signature->GetBufferPointer(), signature->GetBufferSize(), IID_PPV_ARGS(&m_rootSignature)));
}
// Create the pipeline state, which includes compiling and loading shaders.
{
ComPtr<ID3DBlob> vertexShader;
ComPtr<ID3DBlob> pixelShader;
#if defined(_DEBUG)
// Enable better shader debugging with the graphics debugging tools.
UINT compileFlags = D3DCOMPILE_DEBUG | D3DCOMPILE_SKIP_OPTIMIZATION;
#else
UINT compileFlags = 0;
#endif
ThrowIfFailed(D3DCompileFromFile(GetAssetFullPath(L"shaders.hlsl").c_str(), nullptr, nullptr, "VSMain", "vs_5_0", compileFlags, 0, &vertexShader, nullptr));
ThrowIfFailed(D3DCompileFromFile(GetAssetFullPath(L"shaders.hlsl").c_str(), nullptr, nullptr, "PSMain", "ps_5_0", compileFlags, 0, &pixelShader, nullptr));
// Define the vertex input layout.
D3D12_INPUT_ELEMENT_DESC inputElementDescs[] =
{
{ "POSITION", 0, DXGI_FORMAT_R32G32B32_FLOAT, 0, 0, D3D12_INPUT_CLASSIFICATION_PER_VERTEX_DATA, 0 },
{ "TEXCOORD", 0, DXGI_FORMAT_R32G32_FLOAT, 0, 12, D3D12_INPUT_CLASSIFICATION_PER_VERTEX_DATA, 0 }
};
// Describe and create the graphics pipeline state object (PSO).
D3D12_GRAPHICS_PIPELINE_STATE_DESC psoDesc = {};
psoDesc.InputLayout = { inputElementDescs, _countof(inputElementDescs) };
psoDesc.pRootSignature = m_rootSignature.Get();
psoDesc.VS = CD3DX12_SHADER_BYTECODE(vertexShader.Get());
psoDesc.PS = CD3DX12_SHADER_BYTECODE(pixelShader.Get());
psoDesc.RasterizerState = CD3DX12_RASTERIZER_DESC(D3D12_DEFAULT);
psoDesc.BlendState = CD3DX12_BLEND_DESC(D3D12_DEFAULT);
psoDesc.DepthStencilState.DepthEnable = FALSE;
psoDesc.DepthStencilState.StencilEnable = FALSE;
psoDesc.SampleMask = UINT_MAX;
psoDesc.PrimitiveTopologyType = D3D12_PRIMITIVE_TOPOLOGY_TYPE_TRIANGLE;
psoDesc.NumRenderTargets = 1;
psoDesc.RTVFormats[0] = DXGI_FORMAT_R8G8B8A8_UNORM;
psoDesc.SampleDesc.Count = 1;
ThrowIfFailed(m_device->CreateGraphicsPipelineState(&psoDesc, IID_PPV_ARGS(&m_pipelineState)));
}
// Create the command list.
ThrowIfFailed(m_device->CreateCommandList(0, D3D12_COMMAND_LIST_TYPE_DIRECT, m_commandAllocator.Get(), m_pipelineState.Get(), IID_PPV_ARGS(&m_commandList)));
// Create the vertex buffer.
{
// Define the geometry for a triangle.
Vertex triangleVertices[] =
{
{ { 0.0f, 0.25f * m_aspectRatio, 0.0f }, { 0.5f, 0.0f } },
{ { 0.25f, -0.25f * m_aspectRatio, 0.0f }, { 1.0f, 1.0f } },
{ { -0.25f, -0.25f * m_aspectRatio, 0.0f }, { 0.0f, 1.0f } }
};
const UINT vertexBufferSize = sizeof(triangleVertices);
// Note: using upload heaps to transfer static data like vert buffers is not
// recommended. Every time the GPU needs it, the upload heap will be marshalled
// over. Please read up on Default Heap usage. An upload heap is used here for
// code simplicity and because there are very few verts to actually transfer.
ThrowIfFailed(m_device->CreateCommittedResource(
&CD3DX12_HEAP_PROPERTIES(D3D12_HEAP_TYPE_UPLOAD),
D3D12_HEAP_FLAG_NONE,
&CD3DX12_RESOURCE_DESC::Buffer(vertexBufferSize),
D3D12_RESOURCE_STATE_GENERIC_READ,
nullptr,
IID_PPV_ARGS(&m_vertexBuffer)));
// Copy the triangle data to the vertex buffer.
UINT8* pVertexDataBegin;
CD3DX12_RANGE readRange(0, 0); // We do not intend to read from this resource on the CPU.
ThrowIfFailed(m_vertexBuffer->Map(0, &readRange, reinterpret_cast<void**>(&pVertexDataBegin)));
memcpy(pVertexDataBegin, triangleVertices, sizeof(triangleVertices));
m_vertexBuffer->Unmap(0, nullptr);
// Initialize the vertex buffer view.
m_vertexBufferView.BufferLocation = m_vertexBuffer->GetGPUVirtualAddress();
m_vertexBufferView.StrideInBytes = sizeof(Vertex);
m_vertexBufferView.SizeInBytes = vertexBufferSize;
}
// Note: ComPtr's are CPU objects but this resource needs to stay in scope until
// the command list that references it has finished executing on the GPU.
// We will flush the GPU at the end of this method to ensure the resource is not
// prematurely destroyed.
ComPtr<ID3D12Resource> textureUploadHeap;
// Create the texture.
{
// Describe and create a Texture2D.
D3D12_RESOURCE_DESC textureDesc = {};
textureDesc.MipLevels = 1;
textureDesc.Format = DXGI_FORMAT_R8G8B8A8_UNORM;
textureDesc.Width = TextureWidth;
textureDesc.Height = TextureHeight;
textureDesc.Flags = D3D12_RESOURCE_FLAG_NONE;
textureDesc.DepthOrArraySize = 1;
textureDesc.SampleDesc.Count = 1;
textureDesc.SampleDesc.Quality = 0;
textureDesc.Dimension = D3D12_RESOURCE_DIMENSION_TEXTURE2D;
ThrowIfFailed(m_device->CreateCommittedResource(
&CD3DX12_HEAP_PROPERTIES(D3D12_HEAP_TYPE_DEFAULT),
D3D12_HEAP_FLAG_NONE,
&textureDesc,
D3D12_RESOURCE_STATE_COPY_DEST,
nullptr,
IID_PPV_ARGS(&m_texture)));
const UINT64 uploadBufferSize = GetRequiredIntermediateSize(m_texture.Get(), 0, 1);
// Create the GPU upload buffer.
ThrowIfFailed(m_device->CreateCommittedResource(
&CD3DX12_HEAP_PROPERTIES(D3D12_HEAP_TYPE_UPLOAD),
D3D12_HEAP_FLAG_NONE,
&CD3DX12_RESOURCE_DESC::Buffer(uploadBufferSize),
D3D12_RESOURCE_STATE_GENERIC_READ,
nullptr,
IID_PPV_ARGS(&textureUploadHeap)));
// Copy data to the intermediate upload heap and then schedule a copy
// from the upload heap to the Texture2D.
std::vector<UINT8> texture = GenerateTextureData();
D3D12_SUBRESOURCE_DATA textureData = {};
textureData.pData = &texture[0];
textureData.RowPitch = TextureWidth * TexturePixelSize;
textureData.SlicePitch = textureData.RowPitch * TextureHeight;
UpdateSubresources(m_commandList.Get(), m_texture.Get(), textureUploadHeap.Get(), 0, 0, 1, &textureData);
m_commandList->ResourceBarrier(1, &CD3DX12_RESOURCE_BARRIER::Transition(m_texture.Get(), D3D12_RESOURCE_STATE_COPY_DEST, D3D12_RESOURCE_STATE_PIXEL_SHADER_RESOURCE));
// Describe and create a SRV for the texture.
D3D12_SHADER_RESOURCE_VIEW_DESC srvDesc = {};
srvDesc.Shader4ComponentMapping = D3D12_DEFAULT_SHADER_4_COMPONENT_MAPPING;
srvDesc.Format = textureDesc.Format;
srvDesc.ViewDimension = D3D12_SRV_DIMENSION_TEXTURE2D;
srvDesc.Texture2D.MipLevels = 1;
m_device->CreateShaderResourceView(m_texture.Get(), &srvDesc, m_srvHeap->GetCPUDescriptorHandleForHeapStart());
}
// Close the command list and execute it to begin the initial GPU setup.
ThrowIfFailed(m_commandList->Close());
ID3D12CommandList* ppCommandLists[] = { m_commandList.Get() };
m_commandQueue->ExecuteCommandLists(_countof(ppCommandLists), ppCommandLists);
// Create synchronization objects and wait until assets have been uploaded to the GPU.
{
ThrowIfFailed(m_device->CreateFence(0, D3D12_FENCE_FLAG_NONE, IID_PPV_ARGS(&m_fence)));
m_fenceValue = 1;
// Create an event handle to use for frame synchronization.
m_fenceEvent = CreateEvent(nullptr, FALSE, FALSE, nullptr);
if (m_fenceEvent == nullptr)
{
ThrowIfFailed(HRESULT_FROM_WIN32(GetLastError()));
}
// Wait for the command list to execute; we are reusing the same command
// list in our main loop but for now, we just want to wait for setup to
// complete before continuing.
WaitForPreviousFrame();
}
}
The root signature includes a single root parameter: a descriptor table with a range of a single descriptor (for the SRV that describes the texture). The shader visibility is used to prevent broadcasting the root table to all shader cores, since we will only use the SRV from the pixel shader to select a texel from the checkerboard texture (as the per-pixel data to store in the render target). Also, setting root arguments for individual shader stages allows the use of the same binding name across different stages. For example, an SRV binding of t0, SHADER_VISIBILITY_VERTEX and another SRV binding of t0, SHADER_VISIBILITY_PIXEL would be valid. However, if the visibility setting were t0, SHADER_VISIBILITY_ALL for one of the bindings, the root signature would be invalid. That is, if you want each shader to see different textures bound to the same virtual register, the application can define two root parameters using the same slot (for example t0) with distinct visibilities (e.g., VISIBILITY_VERTEX and VISIBILITY_PIXEL). On the other hand, if all shaders are intended to access the same texture, the application can define a single root signature binding to t0, VISIBILITY_ALL.
In the third parameter of CD3DX12_DESCRIPTOR_RANGE1::Init, we specify that the view will be bound to slot 0 reserved for SRVs. Consequently, in this case, we are binding to the virtual register t0.
We won’t make use of dynamic samplers. As mentioned in Hello Triangle, static samplers are part of the root signature but do not contribute to the 64 DWORD limit. In defining the static sampler used by D3D12HelloTextures, we specify D3D12_FILTER_MIN_MAG_MIP_POINT as a filter, indicating the use of a point filter for both texel and mipmap selection.
The texture addressing mode is set to Border, with transparent black as the border color (essentially denoting a transparent color, where the alpha channel is set to 1.0). Observe static samplers impose some limitations on the border colors that can be specified. However, this is not a concern at the moment.
Within the static sampler, we also define the shader visibility (pixel shader) and the slot where we intend to bind it (slot 0 reserved for samplers, thus we will bind it to the virtual register s0). The remaining fields that can be configured for a static sampler are not essential for our current purpose.
In the input layout, we inform the input assembler that the second element\attribute refer to texture coordinates. To this purpose, DXGI_FORMAT_R32G32_FLOAT indicates the vertex attribute consists of two 32-bit floating-point values. We mark it with the semantic name TEXTURE.
In the vertex buffer, , we pair each vertex position with the associated texture coordinates, as illustrated in the final image of the “Texture Coordinate System” section.
Note
At this point, we are ready to create the texture. However, before delving into the details, it’s worthwhile to understand the meaning of the comment associated with the textureUploadHeap variable. The comment emphasizes that a local variable must remain in scope until the command list that references the corresponding resource has completed executing on the GPU. This is crucial because, while we can successfully create resources on GPU heaps from our C++ application, we only receive interface pointers to COM objects to reference them. So, when does a resource actually get destroyed? The answer is surprisingly simple: when our application no longer has any references to it. Thus, if textureUploadHeap were to go out of scope, the destructor of ComPtr would call Release on the underlying pointer to the ID3D12Resource interface. If we had no other references to the resource from our application, the associated physical memory could be reclaimed. However, if this occurs before a command referencing the resource is executed in a command list, undesirable consequences may arise. Fortunately, at the end of the LoadAssets function, we call WaitForPreviousFrame, which halts execution until all commands in the command list have been executed. This ensures that the GPU has processed all commands referencing the resource by the time we exit LoadAssets, permitting textureUploadHeap to go out of scope without any issues.
To create the checkerboard texture and allocate the corresponding memory space, we initialize a D3D12_RESOURCE_DESC structure with the required information. We desire a 2D texture of \(256\times 256\) texels including a single mipmap level (the texture itself), where each texel is a 32-bit value composed of four 8-bit unsigned-normalized integer channels. This can be specified by setting DXGI_FORMAT_R8G8B8A8_UNORM as the texture format. DepthOrArraySize indicates the number of textures (for texture arrays) or the depth (for 3D textures). In this case, we aim for a single 2D texture, so we set this field to 1. You can ignore SampleDesc.Count and SampleDesc.Quality for now.
In the subsequent call to CreateCommittedResource, we allocate sufficient memory space on the default heap to accommodate the texture. However, we need to initialize this memory location with the checkerboard texture data residing in system memory. Therefore, we must allocate additional memory space of the same size on the upload heap to load the texture data created by GenerateTextureData, and then copy it to the memory space allocated on the default heap (remember that we cannot directly access the default heap from the CPU). Note that the resource on the default heap is created with D3D12_RESOURCE_STATE_COPY_DEST, signifying that this resource will be used as the destination of a copy operation. On the other hand, the resource on the upload heap is created with D3D12_RESOURCE_STATE_GENERIC_READ, indicating that we can upload data from the CPU and read it from the GPU, enabling us to employ this resource as the source of a copy operation. Once we copy the texture data from the upload to the default heap (more on this shortly), we no longer require the resource on the upload heap, so textureUploadHeap can go out of scope as mentioned earlier.
Note
You might be wondering why we used GetRequiredIntermediateSize to determine the amount of memory space to allocate on the upload heap. Well, the intermediate resource on the upload heap is only used to store the texture data. In other words, we don’t need to create another texture; a buffer is more than enough. Accordingly, CD3DX12_RESOURCE_DESC::Buffer is employed to create a D3D12_RESOURCE_DESC that describes a buffer. GetRequiredIntermediateSize takes an ID3DResource to compute the amount of memory used by that specific resource. This enables us to pass the texture on the default heap as an argument to calculate the necessary memory size to allocate on the upload heap.
We have already examined how GenerateTextureData generates the checkerboard texture data. We employ this data to initialize the only subresource that constitutes the texture applied to the triangle displayed on the screen (remember that we access resources in memory at a subresource granularity). RowPitch represents the byte size of a row of the subresource, while SlicePitch is the byte size of the entire subresource (at least for 2D subresources; for 3D subresources, it is the byte size of the depth).
UpdateSubresources is a helper function defined in d3dx12.h. It maps a set of subresources from the upload heap to the virtual address space of our C++ application in order to initialize them with subresource data stored in system memory. Subsequently, it records a copy operation on the command list to copy the subresource data from the subresources on the upload heap to the related subresources on the default heap. In this case we have a texture with a single subresource: the texture itself (without additional mipmap levels).
We record (with a command in the command list) a resource state transition to indicate to the GPU that we intend to read the texture on the default heap from the pixel shader. Observe that a (sub)resource must be in D3D12_RESOURCE_STATE_PIXEL_SHADER_RESOURCE before being accessed by the pixel shader via an SRV. Otherwise, if the resource is used with a shader other than the pixel shader, you would need to specify a transition to D3D12_RESOURCE_STATE_NON_PIXEL_SHADER_RESOURCE. This distinction between resources accessed by the pixel shader and other shaders can enable some optimizations. For example, a state transition from D3D12_RESOURCE_STATE_RENDER_TARGET to D3D12_RESOURCE_STATE_NON_PIXEL_SHADER will halt all subsequent shader execution until the render target data is resolved (written). In contrast, transitioning to D3D12_RESOURCE_STATE_PIXEL_SHADER will only block subsequent pixel shader execution, allowing the vertex processing pipeline to run concurrently with render target resolve.
At this point, we can create the view for the texture. To achieve this, a D3D12_SHADER_RESOURCE_VIEW_DESC structure is initialized to specify some important information.
Shader4ComponentMapping specifies a mapping for texel components\channels. It enable a remapping from components of the texels in the texture to components of the vector returned as a result of reading a texel through the corresponding view. The options for each return component are: a component (specified in the range \([0..3]\)) from the SRV fetch result or force 0 or 1. In other words, you can map a channel value in the texel to another channel in the returned result, or set it to 0 or 1, whenever you read a texture by using the corresponding view. The default 1:1 mapping can be specified with D3D12_DEFAULT_SHADER_4_COMPONENT_MAPPING, indicating you want component 0 as the first return component, component 1 as the second return component, component 2 as the third return component, component 3 as the fourth return component.
CreateShaderResourceView creates the SRV and specifies to put it in the first descriptor of m_srvHeap. .
Now, the call to WaitForPreviousFrame at the end of LoadAssets starts to make sense, since we implicitly recorded commands in the command list with the call to UpdateSubresources. It’s a good practice to flush the command queue at the end of the initialization phase before starting to record commands in OnRender (called by the message handler of WM_PAINT). At that point, we no longer require textureUploadHeap, since the GPU has executed the copy operation from the upload heap to the default heap. Therefore, we can exit LoadAssets without any concerns about the scope of the textureUploadHeap variable.
In PopulateCommandList, we pass the GPU handle of the SRV stored in m_srvHeap as root argument for the root table in the root signature. Remember that root tables take byte offsets as root arguments, and indeed a GPU descriptor handle is essentially a byte offset from the start of a descriptor heap. Then, we record a draw command (DrawInstanced) to draw the triangle. The rest of the code is analogous to that examined in previous tutorials.
void D3D12HelloTexture::PopulateCommandList()
{
// ...
// Set necessary state.
m_commandList->SetGraphicsRootSignature(m_rootSignature.Get());
ID3D12DescriptorHeap* ppHeaps[] = { m_srvHeap.Get() };
m_commandList->SetDescriptorHeaps(_countof(ppHeaps), ppHeaps);
m_commandList->SetGraphicsRootDescriptorTable(0, m_srvHeap->GetGPUDescriptorHandleForHeapStart());
m_commandList->RSSetViewports(1, &m_viewport);
m_commandList->RSSetScissorRects(1, &m_scissorRect);
// Indicate that the back buffer will be used as a render target.
m_commandList->ResourceBarrier(1, &CD3DX12_RESOURCE_BARRIER::Transition(m_renderTargets[m_frameIndex].Get(), D3D12_RESOURCE_STATE_PRESENT, D3D12_RESOURCE_STATE_RENDER_TARGET));
CD3DX12_CPU_DESCRIPTOR_HANDLE rtvHandle(m_rtvHeap->GetCPUDescriptorHandleForHeapStart(), m_frameIndex, m_rtvDescriptorSize);
m_commandList->OMSetRenderTargets(1, &rtvHandle, FALSE, nullptr);
// Record commands.
const float clearColor[] = { 0.0f, 0.2f, 0.4f, 1.0f };
m_commandList->ClearRenderTargetView(rtvHandle, clearColor, 0, nullptr);
m_commandList->IASetPrimitiveTopology(D3D_PRIMITIVE_TOPOLOGY_TRIANGLELIST);
m_commandList->IASetVertexBuffers(0, 1, &m_vertexBufferView);
m_commandList->DrawInstanced(3, 1, 0, 0);
// Indicate that the back buffer will now be used to present.
m_commandList->ResourceBarrier(1, &CD3DX12_RESOURCE_BARRIER::Transition(m_renderTargets[m_frameIndex].Get(), D3D12_RESOURCE_STATE_RENDER_TARGET, D3D12_RESOURCE_STATE_PRESENT));
ThrowIfFailed(m_commandList->Close());
}
HLSL#
Now, let’s see what happens in the shader code.
struct PSInput
{
float4 position : SV_POSITION;
float2 uv : TEXCOORD;
};
Texture2D g_texture : register(t0);
SamplerState g_sampler : register(s0);
PSInput VSMain(float4 position : POSITION, float4 uv : TEXCOORD)
{
PSInput result;
result.position = position;
result.uv = uv;
return result;
}
float4 PSMain(PSInput input) : SV_TARGET
{
return g_texture.Sample(g_sampler, input.uv);
}
The shader code reflects the fact that the SRV that describes the checkerboard texture is bound to t0, while the sampler is bound to s0. Also, the PSInput structure now includes the texture coordinates (instead of a color) associated with each vertex position.
In the vertex shader, we simply pass the vertex data to the rasterizer, which interpolates it and subsequently passes the result to the pixel shader.
In the pixel shader, we sample the checkerboard texture using the sampler object bound to s0 and the interpolated texture coordinates. Then, we return the sampled texel as the per-pixel color to be stored in the render target.
Source Code#
D3D12HelloWorld (DirectX-Graphics-Samples)
Support this project
If you found the content of this tutorial somewhat useful or interesting, please consider supporting this project by clicking on the Sponsor button below. Whether a small tip, a one-time donation, or a recurring payment, all contributions are welcome! Thank you!

References#
Microsoft. Introduction to textures in direct3d 11. https://learn.microsoft.com/en-us/windows/win32/direct3d11/overviews-direct3d-11-resources-textures-intro.
Microsoft. Texture addressing modes (direct3d 9). https://learn.microsoft.com/en-us/windows/win32/direct3d9/texture-addressing-modes.
